Discover more from What is wrong with Canadian and American democracies?
Why covered call ETF's rarely work out well for investors
For the promoters they work out just fine
The best way to open this article is to frame the issue in terms of historical stock market returns and the standard deviation of those returns for an extended period. I have chosen the past 50 years. During that time the average return on the S&P 500 stocks was 10.57% and the standard deviation of that return was 17.24%. For any given year in that period, assuming a normal distribution, the range of expected outcomes (95% confidence interval) is from a loss 23.39% to a gain of 45.53%.
Options typically trade at or close the value determined by the Black Scholes option pricing model that won a Nobel prize for its authors Myron Scholes and James Merton. Fisher Black is remembered in the name of the model but died before the Nobel prize was awarded and the Nobel prize is not awarded posthumously. The model, derived from differential equations, essentially found an “equivalence” price where the risk the option premium would be lost in its entirety on expiry was offset by the potential gain if the underlying security traded above the option strike price and generated a return to the option holder. The original model excluded dividends but the updated model accounts for dividends.
Covered call ETF’s speculate that the money received by selling options (the option premium income) is additive to dividends on the portfolio and generates higher income for investors when the lost opportunity from having underlying stocks “called away” by the exercise of the option by its holder is less than the premium income received. That is a bad bet most of the time.
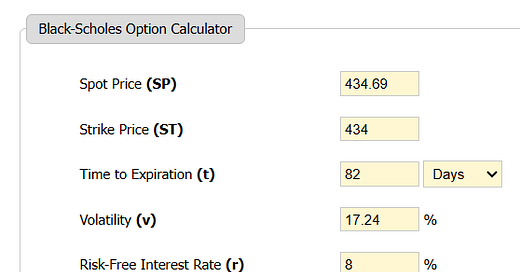
The problem is that ETF active managers are tempted to write options too close the trading price of the underlying stocks to garner the most premium income but ignore the high volatility that risks having the stock called away and missing out on a rapid and sharp rise in trading prices of the shares. The S&P index trust ($SPY) is trading today at $434.69 per unit. A call option on SPY that expires January 24, 2024 is today bid at $13.47 per call with a duration of 82 days.
Using Black-Scholes, the value of that call option is an estimated $17.75 using a risk-free rate of 8%.
Why 8% when ten year treasuries (the typical proxy for a risk-free rate) yield about 4.7%? The answer is that a better analysis is to use the intrinsic risk-free rate which comprises the sum of inflation and GDP growth. The use of treasury rates ignores the reality that the Fed intervenes in the market for bonds and the rate is not a market rate but an administered rate, and investments that yield 4.7% when inflation is running about 3.7% at the most recent report but was 8.2% a year ago and has averaged much higher than 3.7% while current GDP growth is 2.2%. 8% is a sensible figure to use I will argue, since energy prices are rising again and are a primary driver of inflation and the decision of the Fed to pause rate increases risks higher inflation.
My 8% choice comprises a bet that GDP growth of 2% and inflation of 6% is more likely than not. Had I used an intrinsic risk-free rate of 5.9% the B-S model would have returned a value of $16.64 per call.
Writing a call option against the S&P for a premium of $13.34 when the option has an estimated value of about $17.75 or even $16.64 is just a losing bet.
In a recent Bloomberg article, the covered call strategy was called a “Devil’s Bargain” by Quant Roni Israelov. Retail investors are encouraged by advisors to invest in these products which generate relatively high commissions for options trading professionals and fees for ETF managers but produce sub-par returns for investors seduced by the prospect of higher income. Like much of Wall Street, in my opinion it is just another sell-side scam designed to enrich fund managers, advisors and their firms.
Owning long duration calls on beaten down stocks can pay off and limit risk. For example, Canadian Imperial Bank of Commerce ($CM.TO) is now trading at aboutCDN$52 a share, below its book value and down from a peak of close to CDN$80 a share in early 2022. While the bank faces short term pressure from its exposure to Canadian real estate mortgages and overly indebted households generally, it is a well-run bank that rarely trades at a discount to book value. CIBC is not at much risk of failure given Canada’s well-regulated banking system and the supervision of the Office of Superintendent of Banking Institutions (OSFI) and can absorb losses on bad debts without the kind of exposure that brought down American regional banks.
An option on CIBC shares that expires in January 2026 at a CDN$50 strike price trades at about CDN$6 a call option (trading volume is thin so tread carefully). The bet is what price will CIBC shares reach within the roughly two years to maturity of the call? At CDN$56 this investment breaks even, below CDN$50 the option expires worthless, and if CIBC stock trades above CDN$56 there is money to be made. CIBC’s CDN$3.48 dividend is a headwind for option holders since each dividend reduces the share price by an equivalent amount so think of the premium not as CDN$4 a share but as CDN$11 a share, over 20%.
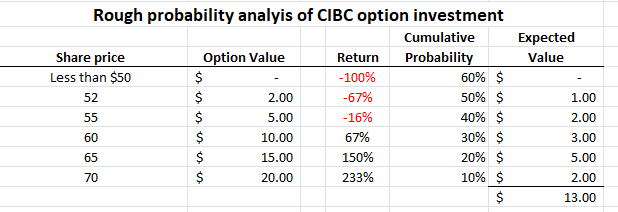
The folowing table shows a range of outcomes. I judge the risk of a total loss on investment to be 60% and the potential for CIBC stock to hit CDN$70 a share during the option term to be 10%. Based on those assumptions, the expected value of the investment is CDN$13 a share, a bit better than a double in just over two years.
A Black-Scholes analysis of the January 6, 2026 CDN$50 call comes up with a value of about CDN$12.50 per call which is consistent with the assigned probabilities in the table shown. I like the bet and hold options on 12,000 shares.
Subscribe to What is wrong with Canadian and American democracies?
The threat to democracy from climate change activism, surging socialism, and identity politics. Investment reviews worth reading.








Dear Mr. Blair,
I'm a big fan of your analysis (many thanks), but in this particular case I believe you a case can be made for the 'risk/reward' evaluation that would cause some investors to prefer to write calls on their stock holdings, thereby, as you say, foregoing the maximum possible upside.
In your CIBC Jan26@50 example, a stockholder would own the stock, collect the 6.7% dividend yield for two years, and lock in an additional $4.00 regardless of outcome (so 100% probability or zero risk), thereby enhancing their outcome by ~4% over simply holding the stock.
For a conservative investor that disparity between the theoretical Black-Scholes value with a greater than 50% chance of a complete loss and the cash in hand might be compelling. And if the stock is likely to be called away after two years (most option contracts are not called before the expiry date), the investor has two options remaining - let it go and reinvest at the higher price with the same strategy (because if the return remains compelling, why not?) or buy back the option and write another at a higher strike price.
Obviously, the rise in excess of $56 wouldn't be captured, but the conservative investor would be in approximately the same investment position as two years earlier. And of course if the stock is below $56 the conservative investor comes out ahead. (This is not to imply that the management expenses with a Covered Call ETF are providing any additional value over 'convenience'.) Thanks!
Your final probability analysis is in error. The obvious single error is that I'm pretty sure you meant to calculate 15 * 20% as 3, not 5. However, I think the problem with your calculation runs deeper in that you shouldn't be multiplying those option values by _cumulative_ probabilities in the first place.